The Collapse is Near : a Video Game Explaining my Thesis

Thanks to my dear colleague and organizer Floriant Sauges from Numana, I had the opportunity to participate in the 2025 Scientific Game Jam, in Montreal, where I teamed up with game designers to translate my research thesis into a playful experience: a video game. After two intense days of development and several more evenings fine-tuning the gameplay, we created “The Collapse is Near.”

• Itch.io : The Collapse Is Near by CogNoman, ManuNeuro, Mounk, Julie and Alexia

Despite its ominous name, The Collapse is Near is not about the collapse of civilization caused by the current catastrophic meta-crisis. Instead, it throws you 5 billion years into the future, where your mission is to save civilization from the imminent collapse of the sun.

The only thing standing between life and destruction is you, your magnetic cannon, and your dexterity in balancing the sun’s state on the razor’s edge of chaos, finding the right amount of order and disorder to load into magnetic waves, displayed on your spaceship’s dashboard. Each second you hold the balance gives Earth a bit more time to survive. Of course, any resemblance to real events is purely coincidental.

Now, since this is a scientific blog, I’d like to dive into the mathematics behind the game, which connect nicely to a key concept from my thesis: the edge of chaos.

Collapse is Near: The Mathematics Behind the Game

The Collapse is Near is an interactive game where players must balance order and chaos to stabilize a dying sun. This challenge is grounded in mathematical principles that echo core ideas from my thesis on balancing order and chaos in recurrent neural networks.

Game Mechanics and Mathematical Concepts

Input and Shannon Entropy

Players interact through keyboard inputs, where we analyze the last 10 keys typed using Shanon entropy:

• This measures the uncertainty or randomness in the sequence of keys.

  \[H(X) = -\sum p(x) \log_2 p(x)\]

  Where $p(x)$ is the probability of character $x$ appearing in the input. Intuitively, higher entropy indicates more unpredictability in your keystrokes (less repetition), which impacts the game’s progression.

For example:

1. If you enter the same letter “AAAAAAAAAA”, $p(A)=1$, and the entropy will be minimum, $H(X)=- 1 \times log_2(1)=0$.
2. If you only input distinct letters “QWERTYUIO”, the entropy will be maximal, $p({Q, W, …})=1/10$, and $H(X)=10 \times (1/10 \times log_2(10))=3.32$.
3. If we considered a more balanced approach, for instance where we had two equally probable characters, like “AAAAABBBBB”, we would have an entropy of $H(X)=2 \times (1/2 \times log_2(2))=1$, a value in between.

Take this into consideration when you try the game!

Entropy Normalization

The computed entropy is then centered around zero and normalized:

This transformation ensures entropy values lie between -1 and 1, reflecting the balance between chaos and order, a perfectly balance entropy have a value of zero. If you look at the gage next to the keyboard in the spaceship, it will reflect the entropy of the last 10 characters, after you pressed the key ENTER.

Magnetic Cannon and Mackey-Glass Equation

Now, the way you control the magnetic canon is by loading it, with either, ordered, or disordered, messages. This will stack up in the entropy load of the canon. The more loaded, the more disordered wave pattern you send to the sun, and the less loaded, the more ordered the wave pattern will be.

The entropy influences the “Entropy Cannon load,” $C$, affecting in turns the sun’s stability:

• $C_{t+1}$ = $\text{Clamp}(C_{t} + \text{Sensitivity} \times H_{norm}, 0, 100)$

So the Canon Load is a percentage value between 0 to 100%. The $Sensitivity$ parameter controls how much the entropy entered at the keyboard will affect the Canon Load :

1. If you take a very high value, the last 10 keys will have a huge influence, and it means you will have to fine tune directly at the keyboard the level of order and disorder, favoring messages with a balanced entropy, close to zero.
2. If you take a very small value, it means the last ten digit entropy doesn’t influence much, so if you want to influence the overall canon load, you should input either very ordered / disordered messages, to change the dynamic of the magnetic wave.

The next step, consists in converting the Canon Entropy load into a parameter ($\tau$), that controls the non-linear equation Mackey-Glass, one of the equation I personnaly used to train and test my neural networks in my two parpers, (1, 2). This equation is a well known benchmark in the field of reservoir computing, in part due to its richness, it can ellicit a wide range of dynamics, from regular to chaotic, depending on parameters.

The Entropy Canon Load, is then converted, to control the Mackey-Glass delay differential equation’s time constant $\tau$:

• Intuition: Lower $\tau$ produces a state $x(t)$ that depends on the recent history, and tends to ellicit regular patterns, essential in stabilizing the sun. Higher $\tau$, on the other hand, means that $x(t)$ will depends on far distant memories, and tends to generate chaotic patterns. In between, $\tau$ ellicit semi periodic wave patterns.
• We have empirically set $\tau_{max}=60$, in order to conserve the monotonicity of the influence of $\tau$ on the dynamic of $x$. Meaning that at some point, even though you continue increasing $\tau$, you will obtain regular dynamics again.
• Remember that there are other parameters, $\beta$, $n$, $\gamma$, all creating very complex and non-linear relations, so controlling the dynamic is not as simple as just pushing a parameter in one or the other direction, hence why we restricted the range of $\tau$ to obtain the desired “linear” control.

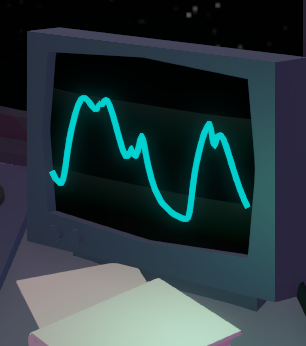	On the right of the spaceship’s dashboard, you have a screen displaying the mackey-glass non-linear dynamical equation, as controlled by the canon load, next converted as the time constant parameter of the equation.

Note: The Mackey-Glass equation is used only for the dashboard visualization, the actual sun mechanics are governed by simpler dynamics.

Sun State Dynamics

Players manipulate wave patterns to regulate the sun’s state by managing the Entropy Load of the magnetic cannon, however, the sun has also its own forces at play:

• The sun’s momentum, representing its internal dynamic, operates as a sinusoid with randomized phase, also influencing its stability, which you can’t influence.

The $\text{sun_state}$ is thus a function of two parameters, its momentum, and the canon influence. It is a quantity, in percentage, that controls the size of the sun, meaning that 0% the sun has completely shrinked, and at 100%, it is completely inflated.

• State Equation:

  \[\text{sun_state}(t+1) = \text{canon_influence}(t) + \text{momentum}(t)\] \[\text{canon_influence} = -(\text{sun_state} - \text{canon_load}) \times \Delta T\] \[\text{momentum}(t) =A\sin(\theta t + \phi) \times \Delta T\]

So, as you can see, the canon influence is not directly the mackey-glass equation, and it’s more simply dependant on the $\text{canon_load}$, in percentage, and the $\text{sun_state}$ :

• If $\text{sun_state} > \text{canon_load}$: cannon shrinks the sun.

• If $\text{sun_state} < \text{canon_load}$: cannon inflates the sun.

Stability is achieved by keeping the sun between 40–60% for five seconds, three times in a row, as you can see in the mission phase display. Exceeding 100% or dropping below 0% results in a loss, either exploding or collapsing the sun!

Thesis Connection

This game serves as a playful implementation of the principles from my thesis, focusing on the interplay of chaos and order in recurrent neural networks, akin to reservoir computing models that optimize computational capability. I have written another article exploring similar concepts from the perspective of cryptopgraphy. There would be so much more to talk about, but this will need a fully dedicated article, so stay tune!