Hash Function with a Chaotic Neural Network

Hi again, everyone! I’m thrilled you’re here because we’re about to dive deeper into an incredible topic: chaotic cryptology.

You can find the code used for generating all the images in my Github.

Since this is the third article in our series potentially leading to a whitepaper in cryptography, I strongly encourage you to read the first two articles on this subject:

• Part1: From ellipitic curve to neural networks
• Part2: Artificial neural networks and percolation

However, let’s do a quick recap of our journey so far.

A Quick Recap, Please?

In our previous discussions, we constructed a neural network with an input layer $X$, a hundred hidden layers, and an output layer $Y$ (see picture below).

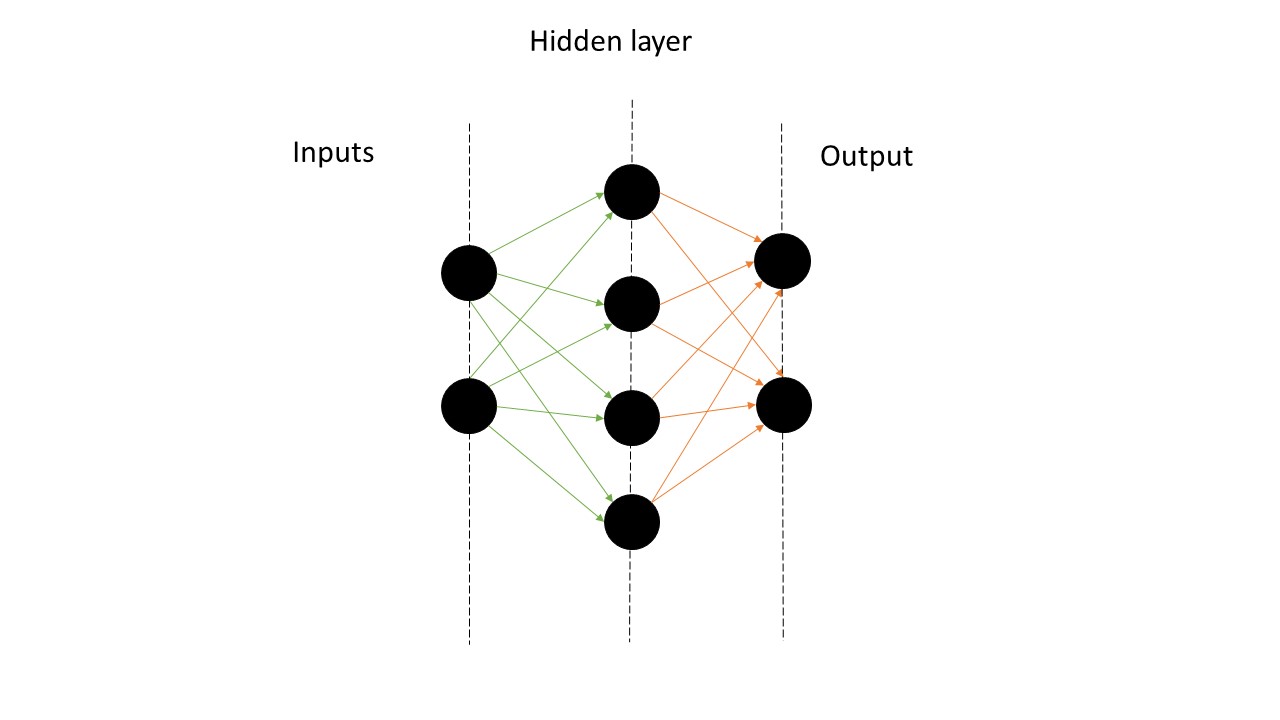
By playing with the weights connecting neurons, we identified a regime above the percolation threshold, which led us to observe a fascinating phase transition from quiescent to active states:

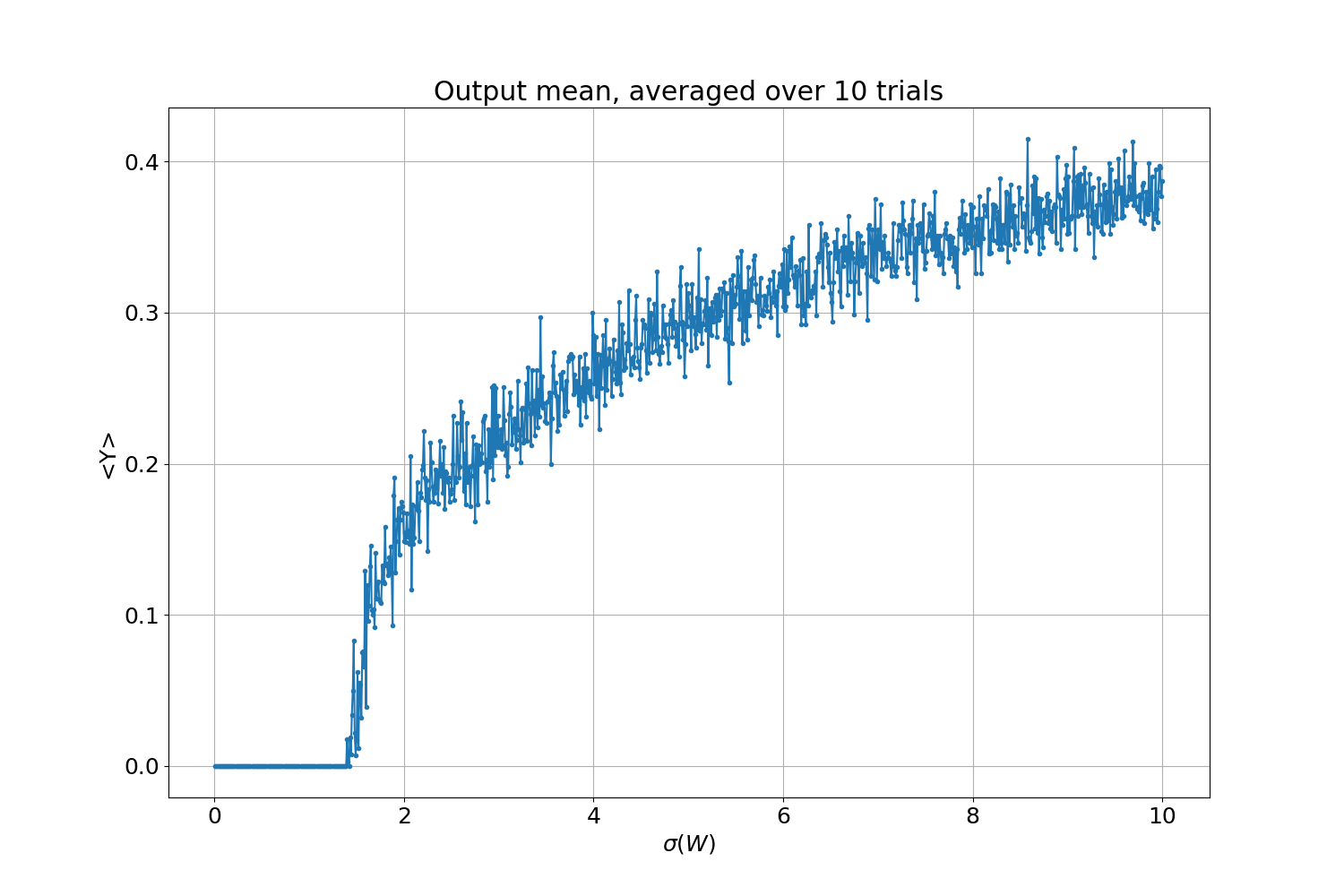
The image above was produced by manipulating the variance of a randomly generated weight distribution. Each dot represents the average output of the network over 10 realizations with different seeds but the same distribution parameters. Concluding our last article, I mentioned that the noise we observed is attributable to sensitivity to initial conditions, a phenomenon known as chaos. This chaos is precisely what we aim to harness for our objectives.

“And what was that objective again?”

Refreshing Our Goal

To refresh our memories kindly, our goal was to design a function $F$ that could establish a deterministic input/output relationship for creating a public_key from a given private_key:

However, we couldn’t settle for just any function because we needed one that would be secure, meaning it should be nearly impossible to find the inverse mapping $F^{-1}$:

We decided to use an Artificial Neural Network (ANN) to encode $F$, opting for $F_{ANN}$ over traditional cryptographic functions like $SHA256$.

Essentially, this was our starting point, and now, there are many more considerations to take into account for the design of $F$, in order to make the encryption process more secure by making it harder to predict or reverse-engineer. Essentially we will talk about two proprties, the confusion and diffusion, which will be key for the design of the neural network:

• Confusion is the property that makes the relationship between the input key and the ciphertext as complex as possible.
  • In other word confusion would be achieved by ensuring that the relationship between the input (e.g., a private key) and the output (e.g., a public key or hash) is highly nonlinear and sensitive to initial conditions, making it difficult to reverse-engineer the input from the output.
• Diffusion, is the property that ensures that the influence of one plaintext symbol is spread over many ciphertext symbols, disguising the statistical properties of the plaintext.
  • Diffusion would be implemented by designing the network such that small changes to the input (or changes in one part of the input) lead to significant and widespread changes in the output, ensuring that the output does not reveal patterns or structures of the input.

Shall we begin?

Artificial Neural Network and the Essence of Confusion

In our journey through the realm of chaotic cryptology, one pivotal aspect we’ve yet to fully explore is the intricate structure of the bit stream $Y$, which emerges from the ANN based on the weights $W$ and the input $X$. Recall that we introduced a binary input vector $X$ into the input layer, aiming to achieve an output $Y=F_{ANN}(X)$. Previously, we visualized $\langle Y \rangle$, the average output across all neurons, to gauge the level of neuron activation. However, this measure alone doesn’t illuminate the system’s potential for encryption, particularly regarding the critical concept of confusion.

Achieving Optimal Confusion

For a cryptographic system to be effective, its output must obscure any discernible structure of the input. Ideally, each bit of the output is an amalgamation of the entire input sequence, rather than being attributable to specific segments of it. This obfuscation ensures that the relationship between the two bit sequences remains concealed.

Feedforward architectures of ANNs are particularly adept at this task. By design, they integrate inputs layer by layer, recursively, which aligns perfectly with our objective. To clarify, consider the following diagram of the ANN architecture we’ve been discussing:

In essence, we can view each layer of the ANN as executing a specific function $F_l$ with a given layer index $l$. This allows us to express the operation of $F_{ANN}$ as a succession of function compositions:

This representation underscores the layered complexity inherent in ANNs, which is fundamental to generating effective confusion. However, the efficacy of this approach is contingent upon the specific operations performed by each function $F_l$, which are, in turn, influenced by the weights $W_l$ at each layer.

Looking Ahead

As we venture further into the application of ANNs in cryptography, our next steps will involve a deeper examination of the functions $F_l$ and the strategic tuning of weights $W_l$. This exploration will be pivotal in harnessing the full potential of ANNs for cryptographic purposes, ensuring that our approach to creating confusion is not just theoretically sound but practically viable.

Tuning Weights for Cryptographic Elegance

The tuning of weights $W_l$ is a critical aspect of machine learning. Yet, in our context, we seek not just to optimize these weights for predictive accuracy but to sculpt them in a manner that maximizes cryptographic security. This endeavor requires a departure from conventional machine learning methodologies, prompting us to consider more nuanced, perhaps even theoretical, approaches to weight adjustment.

Evaluating Confusion in ANNs

To accurately assess the effectiveness of our Artificial Neural Network (ANN) in achieving cryptographic confusion, we require a robust method for measuring how well the output conceals any patterns present in the input signal. Ideally, the output should resemble pure noise, devoid of any discernible structure, thereby ensuring that it reveals nothing about the input.

The Limitation of Traditional Entropy

A common approach to analyzing the structure of binary sequences is through entropy, specifically Shannon entropy. However, for our purposes, Shannon entropy may not provide the full picture. Consider two 16-bit sequences:

At a glance, both sequences have an equal probability of producing a ‘1’ or a ‘0’, leading to the same Shannon entropy value. Yet, intuitively, we recognize a significant difference between the two: $X_1$ is perfectly periodic, while $X_2$ appears more random and unpredictable.

Introducing Binary Entropy ($H_b$)

To address this discrepancy and more accurately measure the quality of confusion, we turn to binary entropy ($H_b$), or BiEntropy, a metric specifically designed to evaluate bit streams. Unlike Shannon entropy, binary entropy excels at distinguishing between ordered and disordered sequences. Let’s consider the binary entropy values for our example sequences:

These values reveal that binary entropy can effectively differentiate between periodic and unpredictable sequences, assigning a value of 0 to fully periodic signals and a value closer to 1 for highly disordered ones. Now you might wonder how this works, and without being too technical, the Bientropy roughly computes the normalized entropy of the $n^th$ derivative of the binary signal, in other word, it quantifies how much predictible is the regularity of the variously spaced patterns in the signal.

The Significance of $H_b$ for Measuring Confusion

The beauty of $H_b$ lies in its range of $[0, 1]$, where 0 indicates complete order and 1 signifies total disorder. This characteristic makes it an ideal metric for evaluating the confusion of an ANN’s output. To prevent the leakage of information about the input, the output should be as indistinguishable from noise as possible. Thus, a higher $H_b$ value, indicating greater disorder, correlates with more effective confusion.

By adopting $H_b$ as our performance metric, we can more accurately gauge the ANN’s ability to obfuscate the input signal, ensuring that the output provides no clues about the original data. This approach not only enhances our understanding of the ANN’s cryptographic robustness but also guides us in fine-tuning the network to maximize security.

The Role of Chaos in Cryptographic Security

In our exploration of artificial neural networks (ANNs) for encryption, understanding the transition from order to chaos—captured through the lens of BiEntropy ($H_b$)—is key. This section delves into how varying the standard deviation of weights, $\sigma(W)$, influences ANNs’ output behavior, crucial for optimizing cryptographic security.

The picture below shows the same phase transition as the plot in the previous article, but this time, as captured by the BiEntropy of the output. For each value of $\sigma(W)$ we ran 100 networks with different seeds.

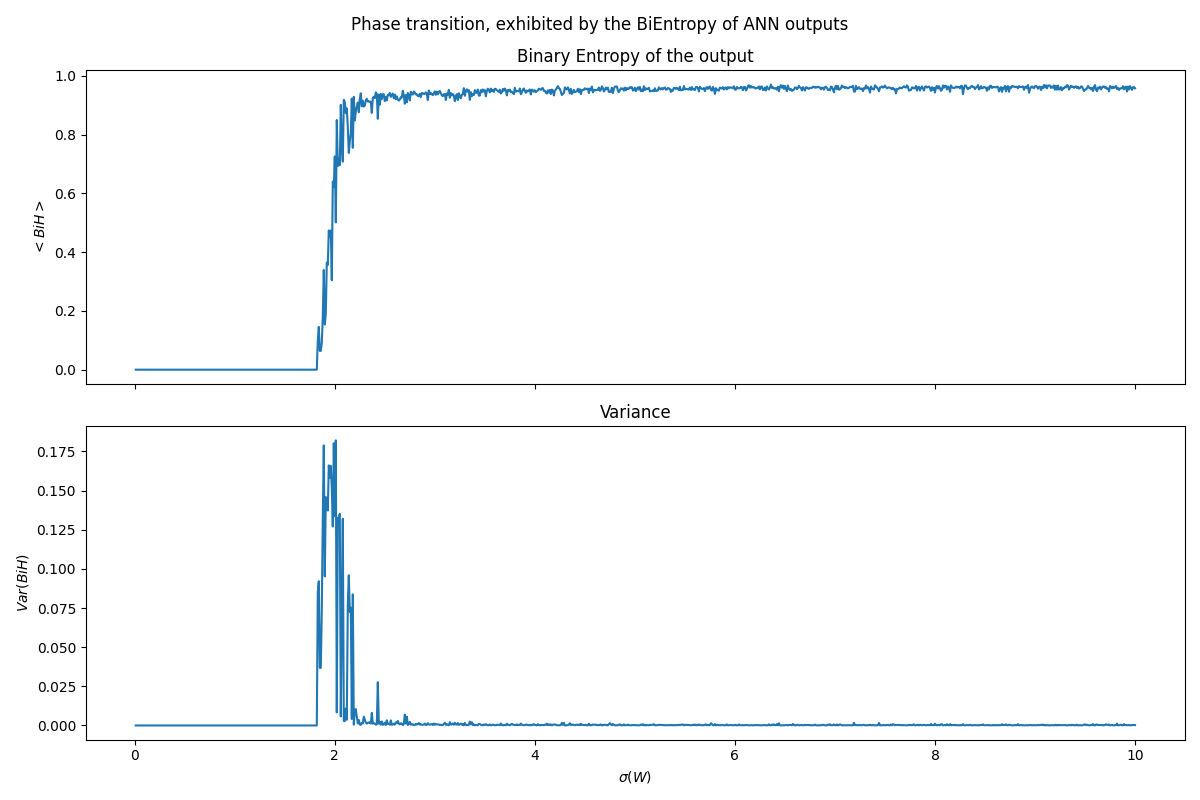
Phase transition, from order to chaos

First, we see that the average of BiEntropy (upper panel) coincides perfectly with the average activity showed in the recap section. The graph reveals a critical phase transition at the percolation threshold, $\sigma_p \sim 1.7$. Below $\sigma_p$, outputs remain ordered with minimal activity while we transition from a quiescent and fully ordered regime with both $\langle Y \rangle=0$ and $\langle H_b\rangle=0$. As $\sigma(W)$ crosses $\sigma_p$, the system enters a chaotic regime, characterized by highly disordered outputs ($\langle H_b\rangle \sim 1$), ideal for encryption due to the maximized confusion and minimized predictability.

The Critical Regime: A Double-Edged Sword

The spike in theBiEntropy variance (lower panel) around $\sigma_p$ marks a “critical regime,” where outputs blend order and disorder. This regime offers potential for neural computation, enhancing memory, separability, and information transmission. However, for encryption, this variability increases mutual information between input and output, potentially compromising security by making the encryption more predictable under certain conditions.

Optimizing Weight Selection for Encryption

To leverage ANNs for robust cryptographic applications, selecting weight statistics that maximize $H_b$ while minimizing its variance is essential. This strategy ensures outputs remain as disordered as possible—enhancing security—while maintaining consistency across network initializations to reduce predictability. So according to our results, the parameter region that is best for encryption is starting from $\sigma > 4$, where the average BiEntropy is the highest, and the variance the lowest, insuring consistency among generaged output. It is important that the variance is low, because we don’t want a network that suddenly produce a more structured output pattern, since it could leak critical information to reverse engineer the hash function!

As we venture further into optimizing our artificial neural network (ANN) for cryptographic applications, a critical consideration emerges—the symmetry between 1s and 0s in the output. Achieving a 50/50 distribution of ones and zeros is paramount to ensuring that no bias skews the output, potentially revealing insights into the underlying structure of our hash function.

The Quest for Balance

The key to achieving this symmetry lies in the delicate balance between excitation and inhibition within the network, as influenced by the variance of weights, $\sigma(W)$. Observations from the output average $\langle Y \rangle$ plot against $\sigma(W)$ illuminate a path towards achieving this balance. As $\sigma(W)$ approaches infinity, the average output intriguingly converges towards $0.5$, symbolizing the ideal equilibrium between ones and zeros. This equilibrium is indicative of a network where excitation and inhibition are perfectly balanced, allowing for an unbiased and secure hash function.

The Role of Weight Distribution

The distribution of positive and negative weights plays a pivotal role in determining the ratio of ones and zeros in the output. Theoretically, the optimal parameter for achieving a symmetric output distribution is when $\sigma(W) \rightarrow \infty$. However, this presents a practical challenge due to the infinite nature of this condition.

Fortunately, a more pragmatic approach exists to attain this symmetry—setting the mean weight, $\mu(W)$, to zero. This approach leverages the inherent symmetry of the Gaussian distribution, where a mean of zero ensures an equal presence of positive and negative weights, thus facilitating the desired balance in the output.

Empirical Validation

To validate this approach, we extend our exploration of $\sigma(W)$ up to $10^{10}$, comparing the outcomes with those obtained when $\mu(W)=0$. The results, depicted in the forthcoming plot (upper panel), demonstrate a remarkable alignment between the empirical data and the theoretical expectation. The green dashed line, representing the scenario with $\mu(W)=0$, aligns seamlessly with the asymptotic values observed for $\sigma(W)>10^6$, underscoring the feasibility of achieving output symmetry through careful weight management.

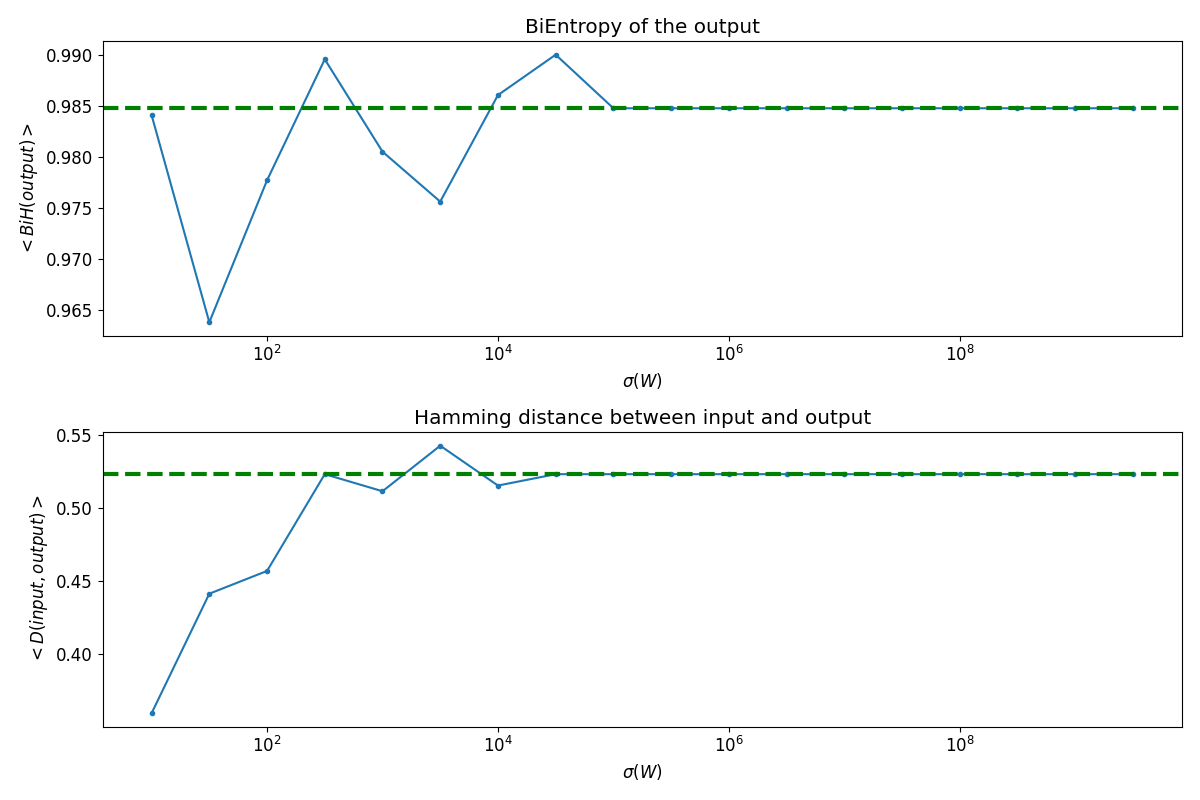
This empirical evidence not only reinforces the theoretical underpinnings of achieving a symmetric output distribution but also provides a practical roadmap for configuring ANNs in a manner that upholds the integrity and security of cryptographic functions.

Enhancing Cryptographic Security through Diffusion

In the quest to fortify the cryptographic robustness of artificial neural networks (ANNs), understanding the dynamics of diffusion—how input influences output—is crucial. This section delves into the Hamming distance as a pivotal metric for assessing diffusion and, by extension, the degree of confusion between input and output sequences.

Understanding the Hamming Distance

The Hamming distance offers a straightforward yet profound measure for evaluating the similarity between two bit streams, $X$ and $Y$. Defined as:

where $N$ is the length of the bit stream, this metric quantifies the number of differing bits between $X$ and $Y$. A value of $0$ indicates perfect inversion (NOT operation) between the sequences, while a value of $1$ signifies identical sequences. The ideal target for uncorrelated sequences, indicative of optimal diffusion, is $0.5$, representing a perfect 50/50 split between matching and non-matching bits.

The Role of Hamming Distance

The Hamming distance measures the number of differing bits between two binary sequences. In the context of ANNs for encryption:

• When assessing diffusion, the Hamming distance between the input and output can indicate how well the system disperses input characteristics across the output. A Hamming distance close to 50% suggests effective diffusion, as it implies that half of the bits differ between the input and output, indicating a good spread of input influence across the output.

• Regarding confusion, while the Hamming distance is not a direct measure, effective diffusion (as indicated by an appropriate Hamming distance) contributes to confusion by complicating the relationship between the input (or plaintext) and output (or ciphertext). When diffusion is effective, it becomes more challenging to identify clear patterns or relationships between the input and output, thereby enhancing confusion.

Insights from Empirical Analysis

The lower panel of the previously referenced figure illustrates the average Hamming distance as $\sigma(W)$ varies. Notably, the distance decreases below $10^2$, suggesting residual correlations between input and output that diminish as $\sigma(W)$ increases. Approaching an asymptote near 50%, we observe the desired randomness indicative of effective diffusion. However, the fully chaotic regime (solid green line) exhibits a slight bias, flipping just over 50% of the bits—a deviation from the ideal.

This observation suggests that while high levels of chaos (e.g., $\sigma(W)$ above $10^2$) enhance diffusion, there exists a nuanced balance. A parameter setting slightly above $10^2$ may offer the closest approximation to the ideal 50% Hamming distance, potentially providing a more secure cryptographic foundation by avoiding predictable biases.

Strategic Implications for Cryptographic Design

The variance observed near the optimal parameter setting underscores the complexity of designing ANNs for cryptography. Rather than a fixed and predictable outcome, a slight variance in the Hamming distance could introduce an additional layer of security, complicating efforts by potential adversaries to decipher or predict the encryption mechanism.

Assessing Cryptographic Integrity through Bit Flipping

In the realm of cryptographic security, merely establishing diffusion between input and output is not the endgame. We must also scrutinize the relationship between different outputs to ensure no exploitable correlations exist. This scrutiny involves an intriguing experiment: flipping a single bit in the input and observing the effect on the output.

The Experiment: Flipping a Single Bit

The essence of this experiment lies in flipping one randomly selected bit in the input and comparing the two resulting outputs. In an ideal cryptographic system, the average Hamming distance between these outputs should be $0.5$. Deviations from this value suggest potential correlations that could compromise the hash function’s integrity.

The Paradox of Machine Learning and Cryptography

Machine learning models, particularly neural networks, are trained to be resilient against minor perturbations, focusing on identifying the underlying patterns amidst noise. This resilience is advantageous for tasks like classification, where the goal is to recognize consistent structures despite variations. However, in cryptography, our objectives are diametrically opposed. A single bit flip in the input should lead to a radically uncorrelated output, transforming the neural network into a change detector where any modification yields a distinct output class.

Chaos: The Ally of Cryptography

Chaos theory, with its hallmark sensitivity to initial conditions, emerges as an invaluable ally in this endeavor. Chaotic systems, by their nature, amplify minor changes in the input through cascading effects, resulting in dramatically different outputs. This property is perfectly aligned with the cryptographic goal of ensuring that even the slightest alteration in the input generates a completely uncorrelated output.

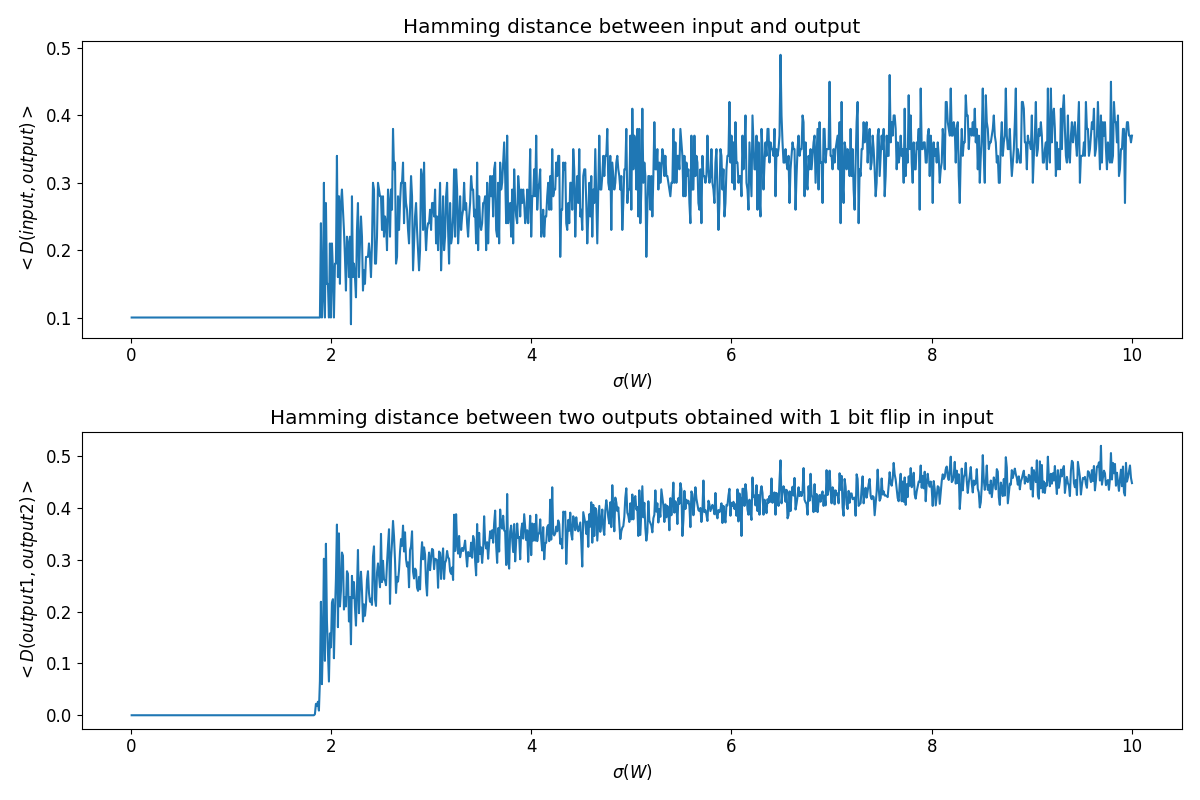
Observations from the Experiment

The depicted phase transition offers a dual perspective on diffusion. The upper panel illustrates diffusion between input and output, while the lower panel reveals the impact of flipping a single input bit on the output correlation.

This analysis highlights a fascinating dynamic: as the control parameter (the standard deviation of weights, $\sigma(W)$) increases, the neural network transitions from a regime where outputs gravitate towards a common attractor—despite input flips—to a chaotic regime. In this chaotic state, even a minor change in the input significantly affects the output, pushing it away from its original attractor.

Conclusion: Embracing Chaos for Cryptographic Security

The experiment underscores the critical role of chaos in enhancing cryptographic security. By leveraging the inherent sensitivity of chaotic systems to initial conditions, we can design neural networks that treat every bit with paramount importance, ensuring that any alteration in the input fundamentally transforms the output. This approach not only fortifies the cryptographic hash function against potential exploits but also exemplifies the intricate balance between predictability and security in the design of cryptographic systems.

Evaluating ANN Against SHA256: A Comparative Analysis

As we draw this comprehensive exploration to a close, it’s crucial to juxtapose our chaotic artificial neural network’s performance with that of a well-established standard in cryptographic hashing: the SHA256 function. This comparison not only provides a benchmark for our ANN’s capabilities but also situates our findings within the broader context of cryptographic technologies.

The SHA256 Function: A Benchmark

SHA256 stands as a cornerstone in cryptographic hashing, renowned for its robustness and widespread adoption. By leveraging Python’s standard library implementation, we can directly compare its diffusion properties against those of our meticulously tuned ANN.

Methodology and Observations

In this comparative analysis, we focus on the diffusion aspect, particularly how each system responds to varying numbers of bit flips in the input. Our objective is to assess the uniformity and unpredictability of the output as we introduce incremental changes to the input.

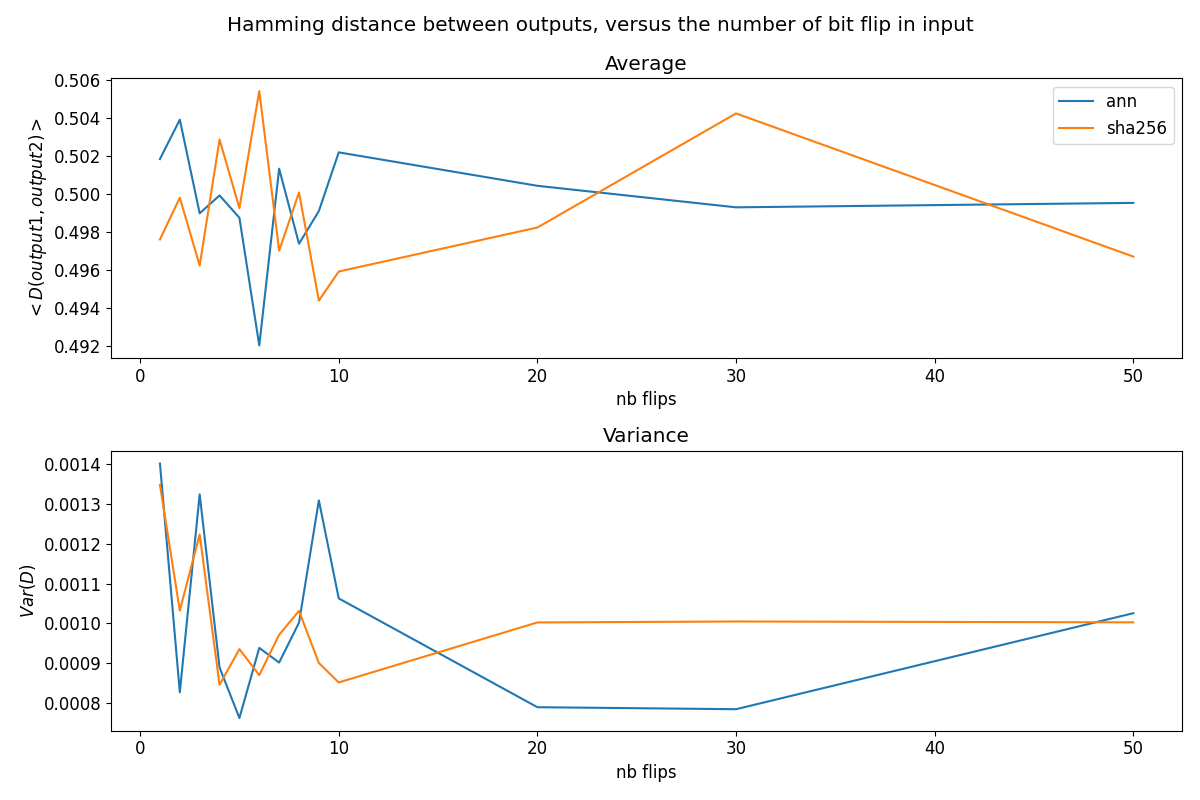
The graph above illustrates a remarkable similarity in the performance of the ANN and SHA256. Notably, both systems maintain a consistent Hamming distance across a range of bit flips—from a single bit to fifty—underscoring their resilience and the absence of any direct correlation between the number of bit flips and the resultant Hamming distance. This consistency is indicative of optimal diffusion, a hallmark of a reliable cryptographic hash function.

Implications for ANN as a Cryptographic Candidate

The neural network’s comparable performance to SHA256, especially under conditions designed to elicit chaos, is both impressive and illuminating. It demonstrates that with the right parameters—specifically, a $\sigma$ tuned to $10^3$ to foster chaos—the ANN can achieve diffusion characteristics on par with SHA256. This finding suggests that the number of bit flips in the input does not materially affect the output’s unpredictability, aligning with the desired attributes of a cryptographic hash function.

However, it’s important to acknowledge that this parity in performance hinges on the ANN’s chaotic behavior, carefully orchestrated through weight distribution. Less chaotic networks exhibit a marked difference in diffusion, with lower Hamming distances for fewer bit flips, gradually increasing as more bits are altered. This behavior underscores the critical role of chaos in achieving cryptographic robustness.

Conclusion: The Potential of Chaotic ANNs in Cryptography

This comparative analysis with SHA256 not only validates the potential of chaotic artificial neural networks in cryptographic applications but also highlights the importance of chaos in ensuring uniform and unpredictable diffusion. As we conclude this exploration, it’s evident that while traditional hash functions like SHA256 set a high standard, chaotic ANNs—when optimally tuned—emerge as viable candidates for advancing the field of cryptographic hashing.

Conclusion: Charting the Future of Cryptography with ANNs

In our journey through the intricate landscape of artificial neural networks (ANNs) as potential cryptographic hash functions, we’ve delved deep into the realms of collision and diffusion tests. These explorations have not only illuminated the capabilities of ANNs in mimicking and potentially rivaling established hash functions like SHA256 but also highlighted the vast, untapped potential that lies within.

The Verdict on ANNs in Cryptography

While our findings are promising, especially the comparative analysis with SHA256, they represent just the tip of the iceberg. Cryptography demands rigor, not just in empirical testing but also in the mathematical underpinnings that guarantee security. Future endeavors should encompass exhaustive collision tests and the development of robust mathematical frameworks to affirm the viability of ANNs in this domain.

The Surprising Versatility of ANNs

The application of AI algorithms, particularly ANNs, in cryptography might initially seem like a leap. Yet, when we consider that both domains thrive on complex diffusion processes and iterative computations, the overlap becomes apparent. ANNs, with their intricate architectures and nonlinear processing capabilities, emerge as natural candidates for crafting sophisticated hash functions.

A New Frontier: Customizable Cryptographic Keys

One of the most compelling aspects of employing ANNs in cryptography lies in the potential for customization. The concept of using random synaptic weight generation, guided by specific keys or seeds, opens up a realm of possibilities. This approach not only adds an additional layer of security by obfuscating the construction of the neural network but also introduces a level of dynamism previously unseen in traditional cryptographic methods.

Looking Ahead

As we stand on the brink of a new era in classical cryptography, potentially threaten by quantum computers, the integration of ANNs presents both challenges and opportunities. The notion of generating unique, secure cryptographic keys through ANNs, tailored to specific tasks and resistant to even quantum computational attacks, is not just a theoretical possibility but a practical horizon we’re beginning to glimpse.

In our next exploration, we will venture further into this promising intersection of cryptography and neural networks. We aim to develop a framework for generating private and public key pairs, using the uniqueness of ANNs to our advantage. This approach, marrying the randomness of synaptic weights with the security requirements of cryptographic keys, could redefine the standards of digital security in the quantum age.

Opérationnel

• On va attendre les tests de bell
• Et tester les systèmes QKD de manière indépendantes en condition réel
• Demander à Bell Francois Raymond (longueur du lien, pertes du lien, et les tables de connexions de dans le patch panel)

Patch panel, prendre une photo

• Comment sont identifiés les ports
• Est-ce qu’on
• Contacter matthieu pour

Fonctionnel: tout le matériel fonctionne, sans aucun soucis technique. Opérationnel:

• Landing pour utilisateur
• Processus
• Accès à distance et locale pour utilisateur

Acheter du matériel

• Acheter un UPS (pour protéger les équipements)

• Les deux disques durs

• Demander à Matthieu ce qu’il se passe quand l’électicité est coupé -> Procédure, qui recoit un message quand ca se coupe? -> Est-ce qu’on a besoin d’une firme?