As I was reading the book: “Mastering Bitcoin” [1], and learning about the generation of public keys, I was captivated by the elliptic curves (see picture below). I couldn’t stop thinking: “I can do that with neural networks!”

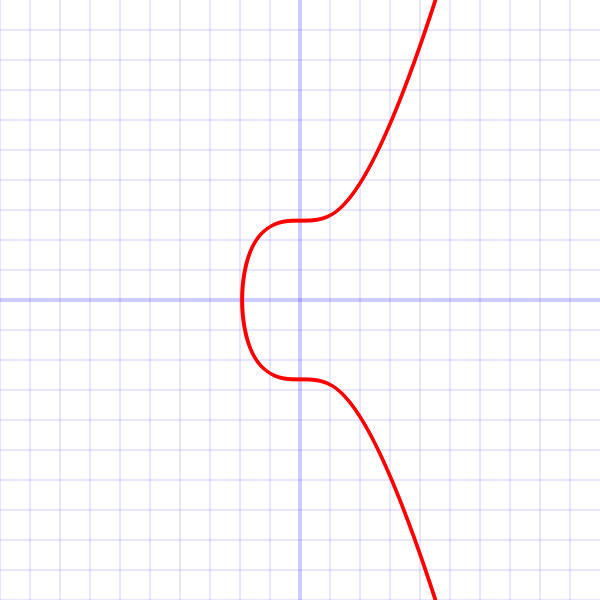
For those who don’t know what I am talking about, I will simplify it as much as possible. In bitcoin, a public key, is used for transactions and is created from a randomly generated private key. No one should ever know the private key because it is the key that allows your funds to be accessed! So the issue here is, how will you verify your identity without compromising your private key? When you use your public key to receive some bitcoins, this must not provide any hint as to what the private key is. Still, it should be uniquely linked to your private key, so only you hold it!

I would formalize the problem this way: when you generate a public key, you need to design a deterministic function $F$, such that:

Ideally, the perfect function would be not-invertible, meaning that $F^{-1}$ does not exist:

A compromise adopted for Bitcoin, is the elliptic curve. It renders nearly impossible the task of finding the inverse. Now, I am not going to dive into too much details, but if you are interested, I invite you to check this very detailed tutorial by Jeremy Kin. The idea is the following: using a generator $G$, on the curve (shown above), the public key is obtained after the multiplication of this point on the curve, private_key times:

Now multiplication on the elliptic curve is obtained by adding G to itself iteratively. Additions on elliptic curves are simple geometric operations, but iterated many steps, they render a very complex input/output relationship. The point here is that even if you know the generator $G$ and the public key, and you try to map back to obtain the private key, the number of possibilities is so daunting that it’s practically impossible to do. Finally, it’s a one-way function, which means that one public key always corresponds to one private key.

Consequently, the elliptic curve is an excellent solution to the problem at hand, and many companies have used it without any issues. However, that’s no reason to stop the exploration for better or original solutions!

So as I was reading the book, I couldn’t stop thinking of using a neural network for encoding $F$. This will be the perfect opportunity to present artificial neural networks in a very non-trivial way, if you dare going down the rabbit hole.

Neo: follow the white-paper, …

To design such a function, I had to keep two essential properties in mind:

• $F$ needs to be deterministic
• $F$ needs to be highly non-linear

For me, neural networks are all about non-linearities. Each neuron consists in applying a non-linear function to its inputs. The picture below shows that a neuron consists of a mathematical functon $f(X, W)$, here displayed as a step function. The neuron receives a weighted sum of inputs. As it is a mathematical function, this neuron is purely deterministic. This is good because it is exactly what you need to design $F$. Second, the state of the neuron $Y$ is binary because below a specific value of $X$, it’s going to give $0$, while above this value, it’s going to give $1$. The output of this function is binary and, as such, non-invertible. Indeed, for the two possible output values $Y\in (0, 1)$, there is an infinite amount of possible values $X$!

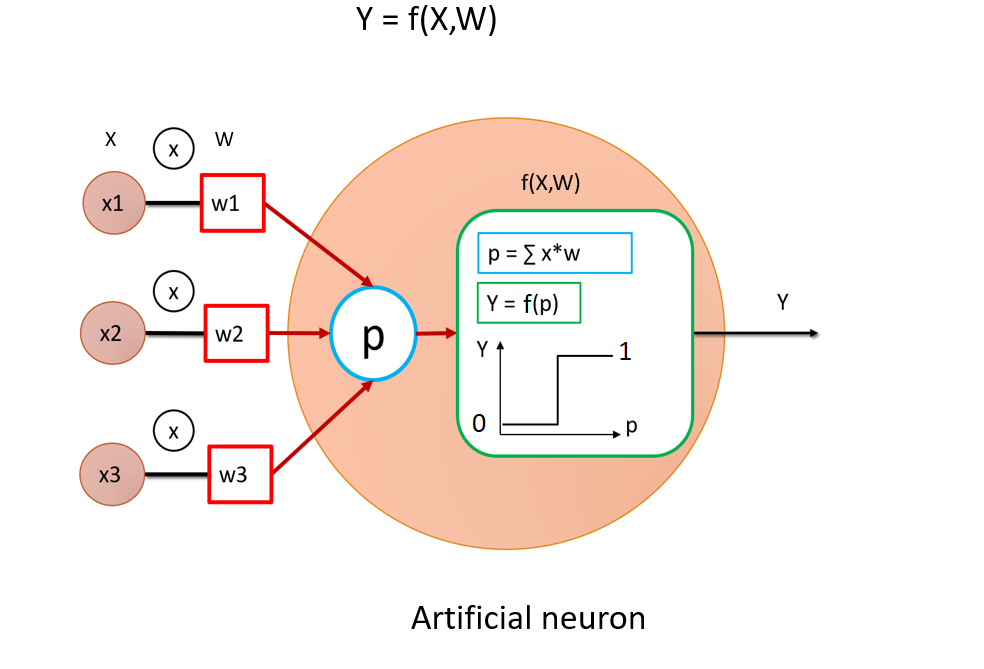
Let’s assume that each input $X=(x1, x2, x3)$ of the neuron is the output of three other neurons, themselves receiving other neuron’s outputs as input. Eventually, we can add many layers of neurons in a cascade to obtain a deep neural network. These neurons create a complex succession of filters, blurring the input space. Hence, there is no chance to deduce the input:

At least, in theory, one could imagine that with enough neurons and complexity in the network, the hyperspace -meaning the encoding space resulting from the aggregation of all these neurons- is virtually infinite. You could potentially create a mapping from any received input to any output you want. Thus you could obtain a deterministic mapping of the two numbers while keeping their resemblance to zero. Well, in theory, yes, and as we will see in practise, it’s a bit more complicated than one might expect.

In general, the Machine Learning (ML) expert’s task is to reduce this hyperspace. He does that by finding the appropriate parameters $W$ of the model, such that the network outputs closely match the targets. Typically, this involves minimizing the error produced by the network’s output through a process called backpropagation. The adapting mechanism tries to find the most efficient way of storing the information in the hyperspace by filtering out everything that is not related to the inputs statistical structure. Put simply; it tries to find correlations among the inputs.

Interestingly, it is the exact opposite thing we need to do here.

We want to design a system that creates an output pattern that is maximally uncorrelated from its input.

Practically, we could frame the problem as if we wanted the network to “learn by heart” a silly list of gibberish and uninteresting words. And who forgot how difficult is this task? I do have my lot of bad memory…

However, to spice things up, I will restrain myself by not using any ML techniques! So no backprop., no cost function minimization, and nothing adaptative at all. We are not taking the blue pill this time, sorry.

To solve this problem, we will get our hands dirty, with some obscure percolation theory, by riding critical phase transitions we will end into pure chaos, aka the red pill.

In the next part 2 we are going to explore how to design an artificial neural network to create the function $F$.

References

[1] Andreas M. Antonopoulos. (2017). Mastering BitCoin Programming the Open Blockchain. In Journal of World Trade (Vol. 50, Issue 4).